Prijavite se za
email obaveštenja Mailing lista
-
kliknite ovde -
Gravitacione mašine
- od Leonarda da Vinčija do najnovijih otkrića
Knjiga koja može menjati svet
PERPETUUM MOBILE
CENA 100 din.
| Veljko Milković • Pronalasci, inovacije, patenti • Samogrejna ekološka kuća, šume za proizvodnju hrane, staklenici, plastenici • Dvostepeni mehanički oscilator - Sistem klatno-poluga • Petrovaradinska tvrđava - podzemlje i nadzemlje, alternativna vodička služba • Svet misterija • Arheološka otkrića • Knjige • Ideje za umetnost, hobi, biznis... | |||||
| Aktuelno | Saradnici | Ideje za umetnost, hobi, biznis... | |||
Nemoguće je često ono što nije pokušano. - Jim Goodwin
"...čudio sam se kako nešto što je tako malo može narasti do takve neizmjerne veličine." - Nikola Tesla
Ovo je tehnički jednostavno, ali mu ne treba olako prići. - Veljko Milković
Novi sajt
DVOSTEPENI MEHANIČKI OSCILATOR - SISTEM KLATNO-POLUGA A
Top 100 Energy Technology in 2006 (by New Energy Congress) Jednostavan mehanizam (slika 1.) ostvaruje nove mehaničke efekte i predstavlja čist izvor energije. Mašina ima samo dva osnovna dela: masivnu polugu i klatno. Interakcija dvostepene oscilacije multiplikuje uloženu energiju podesnu za vršenje korisnnog rada (mehanički čekić, presa, pumpa, transmisija, elektrogenerator...).
Slika 1. Mehanički čekić sa klatnom Najbolji
rezultati su postignuti kada su osovina poluge i klatna na istoj visini
tj. u horizontali, a osovina masivne poluge kada bude iznad centra
mase, kao na gornjoj slici 1. POREKLO ENERGIJE NA BAZI RAZLIKE POTENCIJALA Energija se ostvaruje zahvaljujući razlici potencijala kod postojećih uređaja. Tako potrošači električne energije koriste razliku potencijala između plusa i minusa (jednosmerna struja) i nule i faze kod naizmenične struje. Svi toplotni ili termički motori zahvaljujući većoj temperaturi i pritisku od ambijenta ostvaruju koristan rad. Vodenice i hidroelektrane koriste visinsku razliku vodotoka... Međutim do skoro nije razmatrana razlika potencijala kod dvostepenog oscilatora - "čudnovate mašine"
Slika
2. Razlika potencijala fizičkog klatna pri oscilaciji Kako
postoji razlika potencijala (slika 2.) između bestežinskog stanja
(1) i kulminacije sile (2) pri oscilovanju klatna, isto se događa
i sa centrifugalnom silom koja je ravna nuli u gornjoj poziciji, a
kulminira u donjoj pri maksimalnoj brzini. Fizičko klatno koristi
se kao prvostepeni oscilator u sistemu sa polugom. Merenja Energije Važno je da se primeti da se ne tvrdi da postoji višak mehaničke energije kod oscilatora gde se njegovo klatno inicijalno podigne u početni položaj i pusti da se njiše dok se ne zaustavi. Ideja je da je posle inicijalnog podizanja klatna potrebno dodavati malo energije da bi klatno nastavilo da se njiše. Pošto je dvostepeni oscillator namenjen za duži rad, energija potrebna za inicijalno podizanje klatna može da se zanemari. Logika je ista za Dizel motore gde je potrebno da oni postignu radnu temperaturu pre merenja njihove efikasnosti. Takođe, niko ne uključuje energiju potrošenu za magnetizaciju stalnih magneta u elektromotoru za izračunavanje koeficijenta efikasnosti tog elektro motora. Potrebno je meriti malu energiju neprekidno dodavanu da bi se odžavalo njihanje klatna. Takođe je potrebno primetiti da je izlazna sila na poluzi oscilatora promenljiva i da se menja od nule do maksimuma koji je određen masom na njoj. Razlog za to je promenljiva sila kojom klatno vuče suprotnu stranu poluge. To komplikuje matematički proračun i zato su potrebni precizni istrumenti za merenja sila da bi se izračunao koeficijent efikasnosti oscilatora. Dobro je poznato da se klatno sa fiksiranom tačkom vešanja može klatiti i nekoliko časova. Kod oscilatora je tačka vešanja pokretna. Ona se kreće polukružno u ritmu poluge, čija je frekvencija duplo brža od frekvencije klatna. Kretanje tačke vešanje, ili bolje rečeno ubrzanje, troši energiju klatna koje naglo usporava. Trenje u osovini klatna je zanemarljivo u odnosu na gubitak usled kretanja i ubrzanja tačke vešanja. Oscilatori sa manjim i harmoničnim kretanjima tačke vešanja imaju bolje performanse i zato treba posvetiti posebnu pažnju ovom problemu. Mehanička Fisija Dvostepene mehaničke oscilatore treba postaviti po sistemu geometrijske progresije - čime bi se postigla lančana mehanička reakcija: 1<2<4<8< oscilatora... Slika
3. Eksperimentalni modeli
Ekstremna tehnička rešenja mogu biti turistička atrakcija i na nivou prototipa, bilo u jednostavnijoj ili složenijoj izvedbi.
Dosadašnja iskustva ukazuju na bitnost usklađene frekvencije kod svakog
modela. Održavanje oscilacije fizičkog klatna treba vršiti određenom
brzinom ili se u suprotnom rasipa uložena energija. Predlog za smanjenje trenja Dvostepeni mehanički oscilator ili neki drugi uređaj postaviti u pravcu istok-zapad čime bi se smanjilo aksijalno trenje na ležajevima usled delovanja Koriolisove sile. POSTULATI I DOGME
Najlakše je nešto proglasiti za nemoguće i tako dati olakšicu putem
usvajanja zakona, međutim pitanje je dali su fundamentalni fizički
zakoni savršeni i za sva vremena? Nekome smeta što je ideja jednostavna, a do jednostavnog rešenja se najteže dolazi, a ima i najviše razloga za to.
. Sistem klatno-poluga različit od prostih mašina, bolji od sistema prenosa
FIZIKA DVOSTEPENOG MEHANIČKOG OSCILATORA
Naučna i stručna mišljenja
Matematičke analize
Teorijske analize
Merenja i eksperimenti Veljka Milkovića Energija elastičnog klatna - dokaz ultra efikasnosti?
DALJI EKSPERIMENTALNI RAZVOJ Izveštaj o napretku istraživanja dvostepenog mehaničkog oscilatora Laboratorija za istraživanje dvostepenih mehaničkih oscilacija (ogranak Istraživačko-razvojnog centra Veljko Milković) uspešno razvija "Električni mozak" za oscilacije klatna - sofisticirani multisenzorski sistem za prikupljanje svih neophodnih informacija iz oscilacija i kretanja klatna sa pokretnom tačkom vešanja u cilju dubljeg proučavanja efekata sistema klatno-poluga i buduće automatizacije istog. Razvoj je u završnoj fazi i finalizacija se očekuje u narednim mesecima. Na sledećim slikama možete pogledati sadašnji nivo razvoja ovog uređaja.
. PATENTI
PRAKTIČNA PRIMENA Ručna pumpa za vodu sa klatnom
više informacija o pumpi sa klatnom
Superiornost pogonskog klatna
|
ISTRAŽIVANJE DVOSTEPENIH MEHANIČKIH OSCILACIJA*
*tekst dole je napisan
2001. g. za skorija otkrića pogledajte tekst i video prezentacije gore
POLUGA SA FIZIČKIM KLATNOM KAO PROSTA MAŠINA
Iako je osnovni model, koji je Veljko Milković nazvao "Mehanički čekić sa fizičkim klatnom", već pri prvim ispitivanjima ukazivao na mogućnost da je dobijena energija veća od uložene, Milković se u početku koncentrisao na neposredne praktične mogućnosti tog modela. O tome svedoči i redosled patentnih prijava. Kasnije se ispostavilo da u pogledu iskorišćenja uložene energije i ovaj model predstavlja perpetuum mobile. Međutim, model je energetski otvoren i na izlaznoj i na ulaznoj strani, pa bi egzaktno merenje korisnog dejstva bilo vrlo komplikovano. Pitanje egzaktnog merenja je odloženo, ali je uočena činjenica da model kao takav predstavlja novi oblik proste mašine, te da je zanimljiv i koristan čak i da nema svojstvo uvećanja uložene energije.
U narednom tekstu biće razmotrene one odlike "osnovnog modela" koje ga čine prostom mašinom, ostavljajući za trenutak po strani pitanje koeficijenta korisnog dejstva.
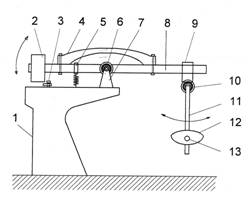
Mehanički čekić sa fizičkim klatnom je originalni uređaj - mašina, koja oscilovanje fizičkog klatna, okačenog na kraju jednog od krakova dvokrake poluge, pretvara u oscilovanje tega na kraju drugog kraka iste poluge. Osa rotacije, osovina fizičkog klatna paralelna je osi rotacije, osovini poluge. Ležište osovine poluge vezano je za podlogu preko nosača. Osovina fizičkog klatna oscilira gore - dole, pošto se klatno izvede iz ravnotežnog položaja. Usled toga oscilira i teg koji se nalazi na kraju drugog kraka poluge. Krak koji pripada fizičkom klatnu podiže se prilikom svakog otklona fizičkog klatna od ravnotežnog položaja, jer se tada težina tega klatna smanjuje, a isti krak poluge se spušta kada je položaj fizičkog klatna blizak ravnotežnom položaju i tako naizmenično. Period oscilovanja poluge i tega koji se na njoj nalazi dvostruko je kraći od perioda oscilovanja fizičkog klatna i tega klatna.
Na slici 1. trougao predstavlja oslonac za dvokraku polugu. Mali kružići su osovine.
Na jednoj osovini osciluje poluga, a na drugoj fizičko klatno. Na desnom
kraku poluge je učvršćena osovina na kojoj osciluje fizičko klatno, a na
levom kraku je pričvršćen teg koji osciluje zajedno sa polugom. Čim se fizičko
klatno izvede iz ravnotežnog položaja i pusti da osciluje, počne da osciluje
i poluga.
Sika 1. Položaj poluge i klatna pri
istovremenoj oscilaciji klatna i poluge
Prinudno oscilovanje tega na polugi može da bude udarnog tipa u slučaju kada teg, na kraju svake oscilacije, poput čekića udara u podlogu ili neki predmet na podlozi. Pri tome, sila udara je veća od one koja održava oscilovanje fizičkog klatna, što još ništa ne govori o bilansu energije jer se delovanje ove dve sile ne odvija u istom vremenskom periodu. Sasvim je nešto drugo ako bi se umesto o sili govorilo o snazi, ali je za to potreban drugačiji pristup.
Veljko Milković je napravio niz eksperimenata na osnovnom modelu - mehaničkom čekiću sa fizičkim klatnom. Svi ti eksperimenti su vodili ka zaključku da je uložena energija manja od energije koju uređaj proizvodi. Kako zakon održanja energije, koji pomaže kod tumačenja skoro svake pojave u fizici, ovde nije mogao da pomogne, dugo se nije ni pokušavalo sa teorijskim razjašnjenjem pojave.
Jedan od mogućih puteva tumačenja vodio je preko delovanja sila koje učestvuju u radu oscilatora. Sile su na neki način konkretnije i prostije fizičke veličine od energije. Međutim, broj sila koje se tu javljaju je velik, one su raznorodne, pa nije lako upoređivati njihova dejstva.
Većina kompetentnih stručnjaka i naučnika koji su detaljno bili upoznati sa Milkovićevim istraživanjima, nije se upuštala u dublju analizu, osim akademika prof. dr Bratislava Tošića. Nažalost, Tošićeva obimna matematička analiza nije donela jasan rezultat u pogledu bilansa energije.
Stručnjaci su se najčešće opredeljivali po osećaju. Neki "za", neki "protiv" perpetuum mobile-a. Među prvima se, nakon izvesnog kolebanja, našao i profesor fizike Nebojša Simin. U početku skeptičan, kao i svi drugi fizičari koji su bili upleteni u ovo istraživanje, Siminov otpor je bio savladan jednim banalnim gestom. Rukom je uhvatio polugu koja je prinudno oscilovala. Klatno je nastavilo da se klati kao da se ništa nije desilo, dok se sa poluge energija prenosila na njegovu ruku. Poluga, znači, neumorno radi, bez vidnog pada oscilatorne energije klatna. Siminu od ovoga nije bio potreban jači i bolji dokaz da se radi o perpetuum mobile-u. Praktično je svejedno da li poluga nešto radi ili ne. Taj rad se ne odražava na oscilaciju klatna, a klatno, sve dok osciluje, izaziva prinudno oscilovanje poluge. Simina je ovo nepovratno uverilo u to da je koeficijent korisnog dejstva poluge sa fizičkim klatnom veći od jedinice. To je istovremeno značilo da zakon održanja energije kod ovog uređaja ne važi i da je ovaj model samo korak do autonomnog perpetuum mobile-a. Da bi model postao autonoman bilo je neophodno smisliti kako deo energije sa poluge vratiti na klatno, da se ono vremenom ne bi zaustavilo usled trenja i otpora vazduha. Milković je i ovo pitanje tehnički razrešio kroz svoje patente.
Nasuprot mišljenju drugih Milkovićevih saradnika i samog Milkovića, Siminu se nije dopadala ideja da se gravitacionom potencijalu pripiše odlučujuća uloga. Ako se zanemari trenje, rad klatna u gravitacionom polju jednak je nuli. S druge strane, niko nije sumnjao u značaj centrifugalne sile klatna. Od samog početka je bilo jasno da je to glavni trag koji treba slediti.
Kod osnovnog modela je mnogo vremena utrošeno na pitanje održanja oscilovanja klatna, s obzirom na sile trenja i otpor vazduha. Milković je to pitanje rešio pomoću elektromagnetnih odbojnika u modelu "Klipna pumpa za vodu sa klatnom i elektromagnetima" , koji je prijavljen 22. februara 2001. godine. Time je kompletiran jedan njegov prethodni model: "Elektrogenerator sa klatnom i magnetnim odbojnicima" , koji je prijavljen 14. jula 2000. godine. Gledano pojedinačno, nijedan od ova dva modela nije autonoman, ali zajedno jesu. Kombinacija ova dva modela predstavlja prvi model perpetuum mobile-a po definiciji.
Milkovića je mučio i problem relativno spore oscilacije klatna, čime se dobija naizmenična struja niske frekvencije. Ovaj problem nije do kraja rešio. Pokušaj sa modelom: "Elektrogenerator sa elastičnom drškom klatna", kod koga se mogu očekivati brže oscilacije, ne rešava problem, jer je u pitanju jednostepeni oscilator kod koga je koeficijent korisnog dejstva manji od jedinice. To je jedini među prvih devet Milkovićevih modela (patenata) koji nema dodirnih tačaka sa perpetuum mobile-om.
"Višak", ili "suficit" energije uglavnom se pripisivao gravitacionom potencijalu. Za skeptike, to je upravo bio "dokaz" da se ne radi o perpetuum mobile-u, jer je rad gravitacionog polja na oscilovanju klatna jednak nuli. To je, po njihovom mišljenju, bilo dovoljno za zaključak da "viška" energije ne može biti. Jedino u čemu su se svi slagali bila je ocena o visokoj efikasnosti uređaja.
Neslaganje oko koeficijenta korisnog dejstva nije moglo da se okonča bez dublje analize. Trebalo je razrešiti pitanje učešća centrifugalne sile fizičkog klatna u oscilovanju poluge, što je bilo očigledno, ali i energetske posledice tog učešća. Ova sila ne učestvuje u oscilaciji klatna, a direktno je odgovorna za oscilaciju poluge. Jasno je da osovina klatna, ako se zanemari njena rotacija, nema kinetičku energiju u sistemu klatna, a ima u sistemu poluge. Međutim, potencijalna energija ove tačke se menja u sistemu poluge. Nije bilo jasno da li ta promena potencijalne energije, uprkos tome što je u toku jedne oscilacije jednaka nuli, ima bilo kakav uticaj na fenomen u celini. Što se tiče rada, klatno vrši rad nasuprot sili trenja i otpora vazduha, a poluga vrši rad, recimo, udarima čekića o podlogu, ili tako što se induktivnim putem proizvodi naizmenična električna struja. Postavljalo se pitanje koji je od ova dva rada veći. Da li rad klatna ili rad poluge. Odgovor se nije mogao dati direktno, jer to podrazumeva egzaktno merenje koje se na originalnom modelu nije moglo izvesti, a ni na ostalim modelima koje je Milković napravio u međuvremenu. Jedan od njih je i lepeza kao dvostepeni oscilator (slika 2.). Lepeza se neobično dugo njiše nakon što se klatno samo jednom izvede iz ravnotežnog položaja. No, teorijsko tumačenje je u ovom slučaju još složenije nego kod osnovnog modela.
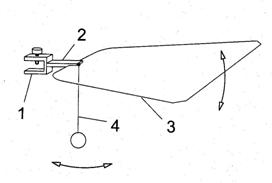
Slika 2. Lepeza
Da se vratimo na osnovni model. U kretanju dvostepenog oscilatora neke stvari se mogu uočiti već na prvi pogled. Između dva međusobno uslovljena ocilatora postoji značajna razlika. Poluga osciluje prinudno, za razliku od klatna. Obrnuto ne ide usled dejstva gravitacione sile na teg klatna. Ako se na klatno veže neki spoljni potrošač energije, klatno ubrzo prestaje sa oscilovanjem, a time i poluga. Ako se, međutim, spoljni potrošač energije veže za polugu, klatno i dalje osciluje. Ako spoljni potrošač energije ne uzme svu raspoloživu energiju poluge, ona će i dalje oscilovati sa nešto smanjenom amplitudom. Ako se pretpostavi da je pozitivan rad poluge, pa tako i njen koristan rad, veći od rada klatna na savladavanju sile trenja i otpora vazduha, dobija se "višak" energije. Taj "višak" može da nastane jedino usled delovanja centrifugalne sile klatna. No, da li je to zaista "višak" energije ili se samo tako čini?
ENERGIJA KLATNA I ENERGIJA POLUGE
Energija je, po definiciji, sposobnost nekog tela da izvrši rad. Energija, dakle, nije nešto što izaziva bilo kakve posledice na bilo čemu, nego ono što bi moglo a i ne mora da izazove posledice u pogledu kretanja drugog tela.
Još kod osnovnog Milkovićevog modela je utvrđeno da promena energije poluge ne izaziva promenu energije klatna. Mehanička energija poluge, u sistemu klatna, jednaka je nuli, pa poluga i ne može da izvrši rad na klatnu. U sistemu podloge, energija poluge je različita od nule, pa može da izvrši rad ukoliko joj se nešto ispreči na putu. Poluga recimo može da izvrši rad udarima o podlogu, ali ni tada neće izvršiti rad na klatnu. Ma šta da se desi sa polugom, energija klatna se neće promeniti.
Energija poluge stoji na raspolaganju spoljnom potrošaču energije, što na energiju klatna ne ostavlja posledice, bilo da poluga nešto radi ili ne. Ako spoljni potrošač preuzme deo ove energije, amplituda oscilovanja poluge će se smanjiti. Kako je poluga ta koja prinudno osciluje, a ne klatno, njeno oscilovanje se nastavlja i kada je delimično prigušeno. Oscilovanje klatna se neometano odvija čak i kada se oscilovanje poluge potpuno priguši. Čim se poluga oslobodi uloge radnog tela, odnosno obaveze da daje energiju spoljnom potrošaču, njeno oscilovanje se odmah ponovo javlja, sa istom onom amplitudom koju je imala pre delimičnog ili potpunog prigušenja. Ovo predstavlja jasan i nedvosmislen znak "viška" energije.
Naime, mehanička energija poluge se javlja bez dodatnog ulaganja energije iz spoljne sredine, zahvaljujući jedino načinu kretanja klatna. Rad poluge ne podrazumeva da klatno treba da izgubi deo svoje energije. Jedino što je potrebno, to je da se klatno klati. S druge strane, klatno se ne klati zato što dobija energiju iz spoljne sredine, nego po inerciji. Drugim rečima, poluga stiče sposobnost da se odrekne dela svoje energije u korist spoljnog potrošača, iako u taj proces nije umešano nikakvo radno telo izvan samog uređaja, a sve pod uslovom da klatno nesmetano osciluje. Podrazumeva se da je klatno prethodno bilo izvedeno iz ravnotežnog položaja. Posle kratkog vremena ova energija u ukupnom radnom, ili energetskom bilansu, ili bilansu snage, može da se zanemari.
Sile trenja i otpor vazduha predstavljale su i u teorijskom i u praktičnom smislu stalni kamen spoticanja, posebno sile trenja i otpora vazduha na klatnu. Milković je ovaj problem rešio posredno, u kombinaciji dva modela.
Ovim se tumačenje rada ovih uređaja oslobađa uvreženih shvatanja o održanju energije. Klasična mehanika ili nije imala u vidu objekte kakvi su višestepeni oscilatori ili je previdela izvesne odlike ovih objekata, ili i jedno i drugo.
Zemljina teža deluje, hteli mi to ili ne,
a na gravitaciju ne možemo uticati jer gravitacioni izolator nije pronađen. Međutim fizičko klatno pri oscilaciji u gornjoj poziciji je više
ili manje u bestežinskom stanju na trenutak.
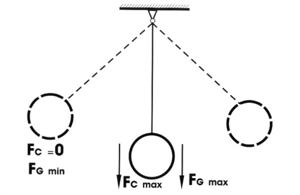
Tako je postignuta zamena za gravitacioni izolator, te je postignuta ultra efikasnost kod dvostepenih oscilatora prikazanih na ovoj kao i na ostalim stranama.
Pored toga eksperimentalno se potvrdila dopunjena formula za kinetičku energiju, kojom se objašnjava suficit energije.
Brzine se sabiraju, što potiče od impulsa, odnosno uložene energije za održavanje klatna u oscilaciji, što se događa u gornjoj poziciji.
Zahvaljujući gravitaciji ostvaruje se dodatno ubrzanje klatna, pa ukoliko se po navedenoj formuli sve izračuna, suficit energije postaje jasan, a potiče od gravitacionog potencijala.
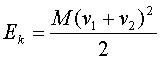
Pored eksperimenata u ovozemaljskim uslovima, izvanredne rezultate su postigle kosmičke sonde, tako da se nije zgoreg podsetiti da je uz pomoć gravitacione sile moguće povećati kinetičku energiju.
English version 
